Aykut Koç‘un grafik sinyal işleme (GSP) üzerine çalışması, yakın zamanda IEEE Transactions on Signal Processing’de yayınlandı.
Grafik sinyal işlemeye (GSP) bu katkıda, Dr. Koç ve işbirlikçileri, kesirli Fourier alanlarında optimal filtreleme problemini grafikler üzerinde formüle etmekte ve GSP için kapalı form çözümünü sunmaktadır. Grafiklerdeki optimal Wiener filtreleme problemini kesirli Fourier alanlarına genelliyoruz. Bu, sıradan Fourier alanlarında karşılık gelen klasik problemin genelleştirilmesidir ve kesirli Fourier dönüşüm sırasını seçmedeki ek serbestlik derecesi sayesinde daha düşük hatalar anlamında gelişmiş performans sunma potansiyeline sahiptir.
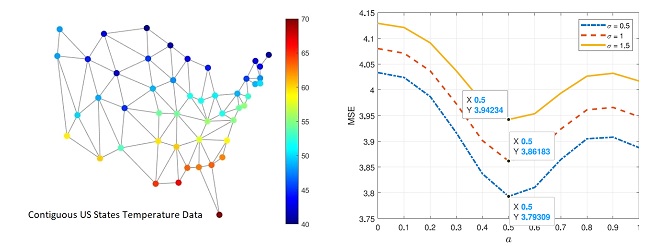
Optimum kesirli Fourier alanı filtreleme problemi teorik olarak GSP çerçevesine genelleştirildi ve kesirli alanlarda filtrelemenin tepe frekansı alanındaki filtrelemeden daha küçük hata değerleri verdiği birkaç sayısal uygulama gösterildi.
Ne grafik yapısında ne de grafik sinyallerinde herhangi bir kısıtlayıcı varsayımda bulunmadık. Bu nedenle, önerilen kesirli grafik Fourier dönüşümü filtreleme çerçevesi, çok çeşitli keyfi koşullar altında uygulanabilir.
Makaleye [buradan] ulaşabilirsiniz.
Özet:
Graph signal processing has recently received considerable attention. Several concepts, tools, and applications in signal processing such as filtering, transforming, and sampling have been extended to graph signal processing. One such extension is the optimal filtering problem. The minimum mean-squared error estimate of an original graph signal can be obtained from its distorted and noisy version. However, the best separation of signal and noise, and thus the least error, is not always achieved in the ordinary Fourier domain, but rather a fractional Fourier domain. In this work, the optimal filtering problem for graph signals is extended to fractional Fourier domains, and theoretical analysis and solution of the proposed problem are provided along with computational cost considerations. Numerical results are presented to illustrate the benefits of filtering in fractional Fourier domains.