Excited to share our latest research published in Signal Processing, introducing the Joint Time-Vertex Fractional Fourier Transform (JFRT), a novel framework that extends traditional joint time-vertex analysis into the fractional domain. By integrating fractional orders in both time and graph domains, JFRT not only generalizes existing Fourier-based methods but also delivers enhanced performance in tasks like denoising, filtering, and clustering.
Key Highlights:
● A unified approach for fractional analysis of joint time-vertex signals.
● Theoretical guarantees including index additivity, reversibility, and reduction to identity.
● A Tikhonov regularization-based denoising method that robustly handles noisy data.
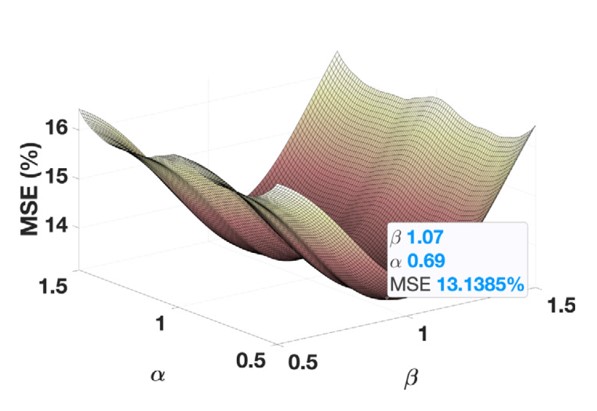
● Comprehensive numerical experiments demonstrating improved results over state-of-the-art techniques.
In summary, our new JFRT method sets a new benchmark for joint time-vertex signal analysis by combining enhanced flexibility, efficiency, and robustness in both time and graph domains. We’re excited about the potential applications of JFRT in advanced graph signal processing and beyond!
#SignalProcessing #GraphSignalProcessing #FractionalFourierTransform
Paper: https://doi.org/10.1016/j.sigpro.2025.109944
Abstract:
Graph signal processing (GSP) facilitates the analysis of high-dimensional data on non-Euclidean domains by utilizing graph signals defined on graph vertices. In addition to static data, each vertex can provide continuous time-series signals, transforming graph signals into time-series signals on each vertex. The joint time-vertex Fourier transform (JFT) framework offers spectral analysis capabilities to analyze these joint time-vertex signals. Analogous to the fractional Fourier transform (FRT) extending the ordinary Fourier transform (FT), we introduce the joint time-vertex fractional Fourier transform (JFRT) as a generalization of JFT. The JFRT enables fractional analysis for joint time-vertex processing by extending Fourier analysis to fractional orders in both temporal and vertex domains. We theoretically demonstrate that JFRT generalizes JFT and maintains properties such as index additivity, reversibility, reduction to identity, and unitarity for specific graph topologies. Additionally, we derive Tikhonov regularization-based denoising in the JFRT domain, ensuring robust and well-behaved solutions. Comprehensive numerical experiments on synthetic and real-world datasets highlight the effectiveness of JFRT in denoising and clustering tasks that outperform state-of-the-art approaches.