Dr. Manouchehr Takrimi’s work on computational electromagnetics has recently been published in IEEE Transactions on Antennas and Propagation.
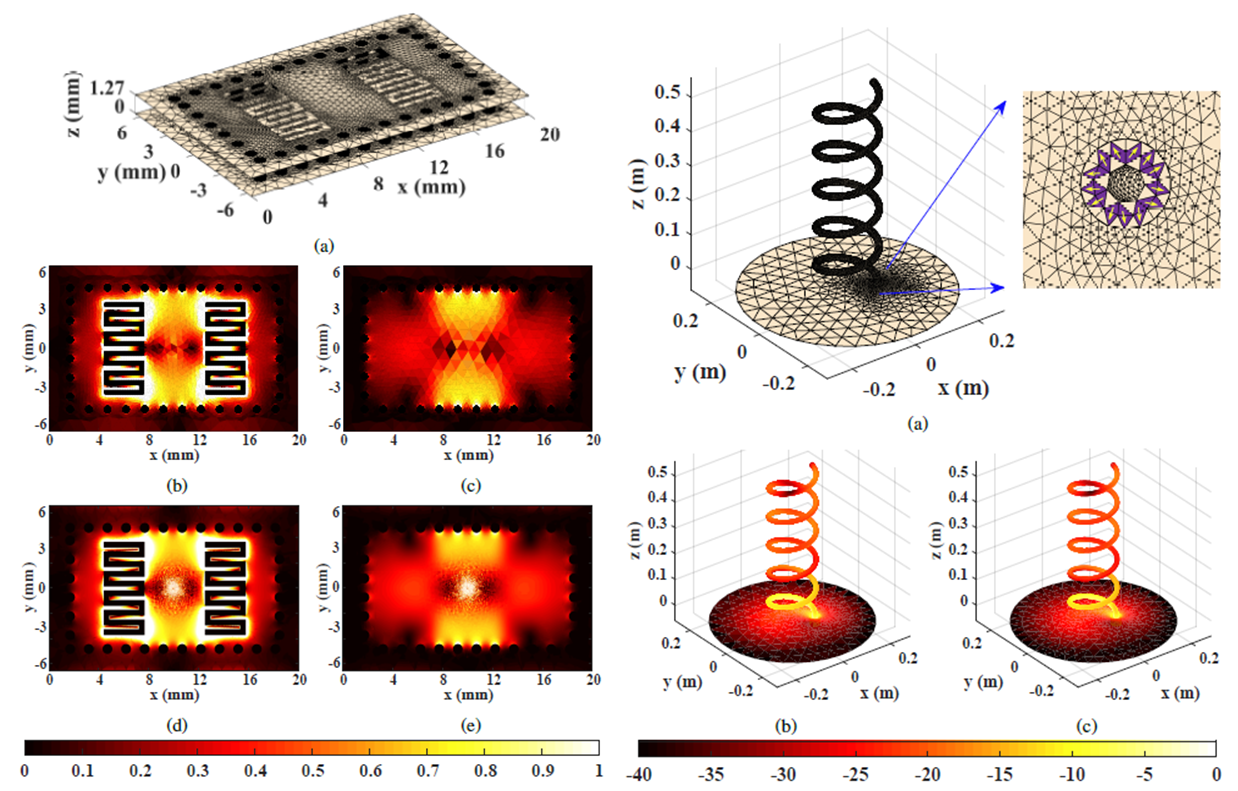
Incomplete tree structures are used in conjunction with the mixed-form multilevel fast multipole algorithm (MLFMA) for the solution of potential integral equations (PIEs) leading to an algorithm that can perform an accurate and efficient analysis of electromagnetic scattering/radiation for multiscale open and closed surfaces. The presented algorithm is also population based and deploys nonuniform clustering for multiscale geometries that are often modeled by using highly variable discretizations. However, it is significantly modified from its original version based on surface integral equations (SIEs) published in 2016, and its modified version for volume integral equations (VIEs) published in 2017. In the recent work, by introducing pruned boxes, and reorganizing box-to-box as well as near- and far-field interactions, the necessary means are provided in order to be combined with PIEs. Numerical results obtained from the scattering/radiation analysis of canonical and real-life multiscale geometries clearly demonstrate the superiority of the algorithm. It is accurate, where the error is controllable, and is very efficient in terms of run-time and especially memory requirements, where more than an order of magnitude saving in memory can be achieved.
The paper can be accessed here.
Abstract: Recently introduced incomplete tree structures for the magnetic-field integral equation are modified and used in conjunction with the mixed-form multilevel fast multipole algorithm (MLFMA) to employ a novel broadband incomplete-leaf (IL) MLFMA (IL-MLFMA) to the solution of potential integral equations (PIEs) for scattering/radiation from multiscale open and closed surfaces. This population-based algorithm deploys a nonuniform clustering that enables to use deep levels safely and, when necessary, without compromising the accuracy resulting in an improved efficiency and a significant reduction for the memory requirements (order of magnitudes) while the error is controllable. The superiority of the algorithm is demonstrated in several canonical and real-life multiscale geometries.