Zipfian regularities are important empirical laws in computational linguistics and natural language processing as well as several other areas of science. Zipf’s law of meaning distribution, one of the most important Zipfian laws, points out a power relation between frequencies of words and number of meanings that words have. In particular, frequent words have more meanings than less frequent words as a result of the Principle of Least Effort. In other words, word frequencies are indicators for polysemy characteristics of words.
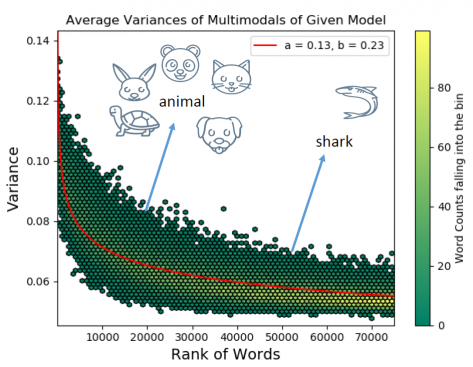
In their paper, KocLab showed that there exists another Zipfian regularity in semantics. It is shown that the generality and specificity of words display a Zipfian regularity when polysemy is neutralized. To measure the specificity levels of words, we utilize variance values of Gaussian embeddings, which is a non-point word representation. By neutralizing the polysemy from the corpus, we obtain Gaussian embeddings of different senses of words and demonstrate the Zipfian pattern in the variance values of words with respect to word frequency ranks. This regularity indicates that “frequent words tend to be more generic, while infrequent words tend to be more specific.”
The paper can be accessed [here].
Abstract:
Being one of the most common empirical regularities, the Zipf’s law for word frequencies is a power law relation between word frequencies and frequency ranks of words. We quantitatively study semantic uncertainty of words through non-point distribution-based word embeddings and reveal the Zipfian regularities. Uncertainty of a word can increase due to polysemy, the word having “broad” meaning (such as the relation between broader emotion and narrower exasperation) or a combination of both. Variances of Gaussian embeddings are utilized to quantify the extent a word can be used in different senses or contexts. By using the variance information embedded in the non-point Gaussian embeddings, we quantitatively show that semantic breadth of words also exhibits Zipfian patterns, when polysemy is controlled. This outcome is complementary to Zipf’s law of meaning distribution and the related meaning-frequency law by indicating the existence of Zipfian patterns: more frequent words tend to be generic while less frequent ones tend to be specific. Results for two languages, English and Turkish that belong to different language families, are also provided. Such regularities provide valuable information to extract and understand relationships between semantic properties of words and word frequencies. In various applications, performance improvements can be obtained by employing these regularities. We also propose a method that leverages the Zipfian regularity to improve the performance of baseline textual entailment detection algorithms. To the best of our knowledge, our approach is the first quantitative study that uses Gaussian embeddings to examine the relationships between word frequencies and semantic breadth.