Dr. Aykut Koç’s work on graph signal processing (GSP) has recently been published in IEEE Transactions on Signal Processing.
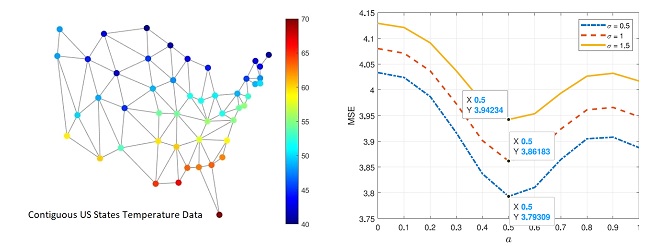
In this contribution to the graph signal processing (GSP), Dr. Koç and his collaborators formulate the problem of optimal filtering in fractional Fourier domains on graphs and provide closed form solution of it for GSP. We generalize the optimal Wiener filtering problem on graphs to fractional Fourier domains. This is the generalization of the corresponding classical problem in ordinary Fourier domains, and has the potential to offer improved performance in the sense of lower errors, thanks to the additional degree of freedom in choosing the fractional Fourier transform order.
The optimal fractional Fourier domain filtering problem has been theoretically generalized to GSP framework and several numerical applications in which filtering in fractional domains yields smaller error values than filtering in the vertex-frequency domain have been demonstrated.
Neither on the graph structure nor on the graph signals, did we make any restrictive assumptions. Therefore, the proposed fractional graph Fourier transform filtering framework can be applied under a wide variety of arbitrary conditions.
The paper can be accessed [here].
Abstract:
Graph signal processing has recently received considerable attention. Several concepts, tools, and applications in signal processing such as filtering, transforming, and sampling have been extended to graph signal processing. One such extension is the optimal filtering problem. The minimum mean-squared error estimate of an original graph signal can be obtained from its distorted and noisy version. However, the best separation of signal and noise, and thus the least error, is not always achieved in the ordinary Fourier domain, but rather a fractional Fourier domain. In this work, the optimal filtering problem for graph signals is extended to fractional Fourier domains, and theoretical analysis and solution of the proposed problem are provided along with computational cost considerations. Numerical results are presented to illustrate the benefits of filtering in fractional Fourier domains.