Please check our new article at the intersection of machine learning and signal processing published at IEEE Signal Processing Letters!
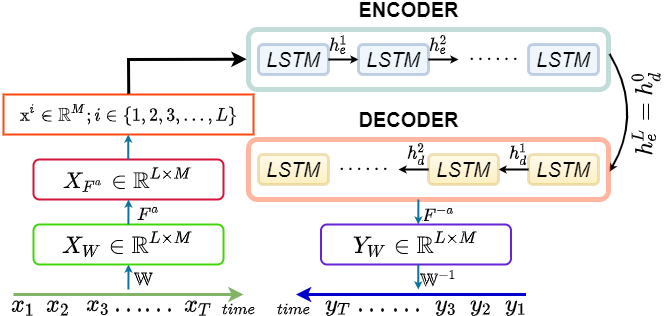
We extend the theory of FrFT, a parametric signal transformation, by introducing it as a trainable layer in neural network architectures. We showed that the transformation parameters can be learned along with the remaining network weights through backpropagation during the training stage. Having established the theoretical foundation for this concept and validated through comprehensive experiments across distinct tasks, our work encourages the integration of numerous other parametric signal processing tools into neural networks.
Paper: https://ieeexplore.ieee.org/document/10458263
Code: https://github.com/koc-lab/TrainableFrFT
Abstract:
Recently, the fractional Fourier transform (FrFT) has been integrated into distinct deep neural network (DNN) models such as transformers, sequence models, and convolutional neural networks (CNNs). However, in previous works, the fraction order a is merely considered a hyperparameter and selected heuristically or tuned manually to find the suitable values, which hinders the applicability of FrFT in deep neural networks. We extend the scope of FrFT and introduce it as a trainable layer in neural network architectures, where a is learned in the training stage along with the network weights. We mathematically show that a can be updated in any neural network architecture through backpropagation in the network training phase. We also conduct extensive experiments on benchmark datasets encompassing image classification and time series prediction tasks. Our results show that the trainable FrFT layers alleviate the need to search for suitable a and improve performance over time and Fourier domain approaches. We share our publicly available source codes for reproducibility.